Rating to percentage formula
Introduction
Main character stats like Might, Agility, etc. are like containers. They contain contributions to the stats that really influence your character's performance. These stats can be like Morale, having a direct effect, or various ratings.
Ratings are indirect, in the sense that they provide the base for the calculation of a number of characteristics. Examples of these ratings are Critical Rating, Physical Mastery Rating, Resistance Rating, etc.
Ratings are in turn converted by a formula to percentages (and this can be multiple percentages from a single rating). These percentages then are having the direct effect for having for example a chance at something (scoring a critical hit or parrying an opponent's attack, etc.) or as an enhancement factor (increasing your weapons damage or decreasing the amount of damage received).
Curved graph

The formulas which the game is using for these conversions, do not result in a linear graph. Instead of a straight rating to percentage calculation, by multiplication of a factor, it's using curved graphs like in the figure above. This has the following properties which are considered an advantage:
- low stats are "boosted". good for starting players.
- advanced players with good gear are at the top of the curve and get relatively less from any more advancements. they need to work hard to reach the maximum (if this is possible).
For the game developers, it also has some other advantages:
- by changing the bending in the curve, they can influence the height of the average result.
- by the amount of bending in the curve, they can concentrate the result, so that most people's stats are kind of the same.
Percentage Caps

Percentages from ratings are in most cases "capped". This means that a rating percentage (P) has a maximum (Pcap). However, the amount of rating (R) that you can have, is never restricted. It's just not usefull to have more than the required rating to reach the cap (Rcap).
Putting a "hard" maximum on a percentage programmatically (Hard-Pcap) is not the only way to limit a percentage. The calculation formula itself has the property to limit the resulting percentage. This mathematical cap (Soft-Pcap) is unreachable by any rating: the curve will always stay under that limit.
Player level
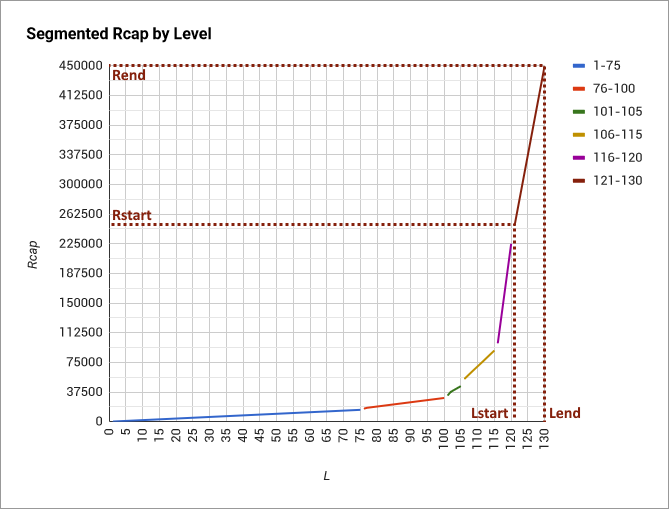
The amount of rating needed to reach percentage caps (Rcap) is raised with level increase of the player. This is to provide a continuing challenge to the player. This means that whenever a player levels up:
- Rcap increases by a fixed amount.
- consequently with the same rating, the rating to percentage formula outputs to a lower percentage.
- a player needs to increase his rating to keep the same percentage, thus providing the challenge of getting better gear with better stats.
As you can see in the example figure, the graphs for Rcap is a straight line (constant rating increases per level), but over the whole level span this is segmented. The reason for this is in direct connection with the difficulty of the game on various levels. And game difficulty depends in turn on the various game expansions which were developed for certain level segments.
Formulas
B-rating (B)
B-rating and not the cap rating (Rcap) is used in the calculations. This formula can be used to calculate the B-rating from a straight line between two progression points (Lstart,Bstart) - (Lend,Bend) where Lstart <> Lend:

- Lstart = start point combat level.
- Lend = end point combat level.
- Bstart = start point B-rating.
- Bend = end point B-rating.
- L = combat level. For stats in the character panel this is always the player's level, but your opponent's level plays a major roll as well in reality.
Percentage from rating (P)
This is the curve formula which is used for the rating to percentages conversion:

- A = soft percentage cap (Soft-Pcap).
- B = B-rating.
- R = rating amount.
For percentages in the character panel, you'll need to add 0.0002 to this formula's result to be accurate. It's unknown if this only for display purposes (rounding errors) or if this is used for calculations as well.
The resulting percentage of this formula should be capped by Pcap.
Rating from percentage (R)
This formula can be used to calculate the required rating for a given percentage:

- A = soft percentage cap (Soft-Pcap).
- B = B-rating.
- P = desired percentage for which to calculate the rating amount.
The resulting rating of this formula should be capped by Rcap.
Required rating for percentage cap (Rcap)
The cap rating can be calculated by using the rating formula and using the cap percentage as percentage:

- A = soft percentage cap (Soft-Pcap).
- B = B-rating.
- Pcap = hard percentage cap (Hard-Pcap).
Usually, Rcap is equal to B-rating because the Curve Constant is often 1 (Hard-Pcap = Soft-Pcap / 2). Exceptions are mitigations and Critical/Devastating Hit Magnitude.
Curve constant (C)
This formula can be used to calculate the curve constant:

- Pcap = hard percentage cap (Hard-Pcap).
- A = soft percentage cap (Soft-Pcap).
The Curve constant is a measure of the bending of a curve. If it's positive then the curve bends down, if it's negative then the curve's slope goes up and if the curve constant is zero then it's not a curve but a straight line.

Optimal Rating (Roptimal)
This formula can be used to calculate the optimal rating:

- C = Curve constant
- Rcap = cap rating
The optimal rating is the rating pivot point where you have the most percentage profit from the curve versus a straight line. For many rating percentages with C=1 this is (SQRT(2)-1)*Rcap.
Ratings Graph Data
This table shows all the information which is needed for calculations. For to find the right information row:
- Locate the needed rating percentage.
- Search the right segment for your level between LvlSeg Start and LvlSeg End (LvlSeg Start < Level <= LvlSeg End).
Explanation of the columns:
- Pbonus = a bonus percentage which needs to be added to the percentage formula result.
- Level = what combat level to use in the B-rating formula? Highest: maximum of both sides. Lowest: minimum of both sides. CharLvl: player's level. OppLvl: opponent's level. This is highly speculative for most percentages, except for mitigations.
The resulting B-rating needs to be rounded:
- lvl 1-50: 0 decimals
- lvl 51-105, 116-130: -1 decimals (10s)
- lvl 106-115, 131-150: -2 decimals (100s)
| LvlSeg Start | LvlSeg End | Pcap | A | Bstart | Bend | Lstart | Lend | Pbonus |
|---|---|---|---|---|---|---|---|---|
| Critical Hit Chance (Critical Rating) by OppLvl* | ||||||||
| 1 | 50 | 25 | 75 | 300 | 3,000 | 1 | 50 | 0 |
| 50 | 60 | 25 | 75 | 3,000 | 4,500 | 50 | 60 | 0 |
| 60 | 65 | 25 | 75 | 4,500 | 6,000 | 60 | 65 | 0 |
| 65 | 75 | 25 | 75 | 6,000 | 9,000 | 65 | 75 | 0 |
| 75 | 85 | 25 | 75 | 9,000 | 13,500 | 75 | 85 | 0 |
| 85 | 95 | 25 | 75 | 13,500 | 19,500 | 85 | 95 | 0 |
| 95 | 100 | 25 | 75 | 19,500 | 27,100 | 95 | 100 | 0 |
| 100 | 105 | 25 | 75 | 27,100 | 36,000 | 100 | 105 | 0 |
| 105 | 106 | 25 | 75 | 36,000 | 40,000 | 105 | 106 | 0 |
| 106 | 115 | 25 | 75 | 40,000 | 54,000 | 106 | 115 | 0 |
| 115 | 116 | 25 | 75 | 54,000 | 62,000 | 115 | 116 | 0 |
| 116 | 120 | 25 | 75 | 62,000 | 68,000 | 116 | 120 | 0 |
| 120 | 121 | 25 | 75 | 68,000 | 78,000 | 120 | 121 | 0 |
| 121 | 130 | 25 | 75 | 78,000 | 102,000 | 121 | 130 | 0 |
| 130 | 131 | 25 | 75 | 102,000 | 117,000 | 130 | 131 | 0 |
| 131 | 140 | 25 | 75 | 117,000 | 204,000 | 131 | 140 | 0 |
| 140 | 141 | 25 | 75 | 204,000 | 265,000 | 140 | 141 | 0 |
| 141 | 150 | 25 | 75 | 265,000 | 450,000 | 141 | 150 | 0 |
| Devastating Hit Chance (Critical Rating) by OppLvl* | ||||||||
| 1 | 50 | 10 | 30 | 400 | 4,000 | 1 | 50 | 0 |
| 50 | 60 | 10 | 30 | 4,000 | 6,000 | 50 | 60 | 0 |
| 60 | 65 | 10 | 30 | 6,000 | 8,000 | 60 | 65 | 0 |
| 65 | 75 | 10 | 30 | 8,000 | 12,000 | 65 | 75 | 0 |
| 75 | 85 | 10 | 30 | 12,000 | 18,000 | 75 | 85 | 0 |
| 85 | 95 | 10 | 30 | 18,000 | 26,000 | 85 | 95 | 0 |
| 95 | 100 | 10 | 30 | 26,000 | 36,000 | 95 | 100 | 0 |
| 100 | 105 | 10 | 30 | 36,000 | 48,000 | 100 | 105 | 0 |
| 105 | 106 | 10 | 30 | 48,000 | 53,000 | 105 | 106 | 0 |
| 106 | 115 | 10 | 30 | 53,000 | 72,000 | 106 | 115 | 0 |
| 115 | 116 | 10 | 30 | 72,000 | 83,000 | 115 | 116 | 0 |
| 116 | 120 | 10 | 30 | 83,000 | 90,000 | 116 | 120 | 0 |
| 120 | 121 | 10 | 30 | 90,000 | 104,000 | 120 | 121 | 0 |
| 121 | 130 | 10 | 30 | 104,000 | 135,000 | 121 | 130 | 0 |
| 130 | 131 | 10 | 30 | 135,000 | 155,000 | 130 | 131 | 0 |
| 131 | 140 | 10 | 30 | 155,000 | 270,000 | 131 | 140 | 0 |
| 140 | 141 | 10 | 30 | 270,000 | 350,000 | 140 | 141 | 0 |
| 141 | 150 | 10 | 30 | 350,000 | 600,000 | 141 | 150 | 0 |
| Critical & Devastating Hit Magnitude (Critical Rating) by OppLvl* | ||||||||
| 1 | 50 | 75 | 225 | 600 | 6,000 | 1 | 50 | 0 |
| 50 | 60 | 75 | 225 | 6,000 | 9,000 | 50 | 60 | 0 |
| 60 | 65 | 75 | 225 | 9,000 | 12,000 | 60 | 65 | 0 |
| 65 | 75 | 75 | 225 | 12,000 | 18,000 | 65 | 75 | 0 |
| 75 | 85 | 75 | 225 | 18,000 | 27,000 | 75 | 85 | 0 |
| 85 | 95 | 75 | 225 | 27,000 | 39,000 | 85 | 95 | 0 |
| 95 | 100 | 75 | 225 | 39,000 | 54,000 | 95 | 100 | 0 |
| 100 | 105 | 75 | 225 | 54,000 | 72,000 | 100 | 105 | 0 |
| 105 | 106 | 75 | 225 | 72,000 | 79,000 | 105 | 106 | 0 |
| 106 | 115 | 75 | 225 | 79,000 | 108,000 | 106 | 115 | 0 |
| 115 | 116 | 75 | 225 | 108,000 | 124,000 | 115 | 116 | 0 |
| 116 | 120 | 75 | 225 | 124,000 | 135,000 | 116 | 120 | 0 |
| 120 | 121 | 75 | 225 | 135,000 | 155,000 | 120 | 121 | 0 |
| 121 | 130 | 75 | 225 | 155,000 | 203,000 | 121 | 130 | 0 |
| 130 | 131 | 75 | 225 | 203,000 | 233,000 | 130 | 131 | 0 |
| 131 | 140 | 75 | 225 | 233,000 | 410,000 | 131 | 140 | 0 |
| 140 | 141 | 75 | 225 | 410,000 | 530,000 | 140 | 141 | 0 |
| 141 | 150 | 75 | 225 | 530,000 | 900,000 | 141 | 150 | 0 |
| Finesse (Finesse Rating) by OppLvl* | ||||||||
| 1 | 50 | 50 | 150 | 200 | 2,000 | 1 | 50 | 0 |
| 50 | 60 | 50 | 150 | 2,000 | 3,000 | 50 | 60 | 0 |
| 60 | 65 | 50 | 150 | 3,000 | 4,000 | 60 | 65 | 0 |
| 65 | 75 | 50 | 150 | 4,000 | 6,000 | 65 | 75 | 0 |
| 75 | 85 | 50 | 150 | 6,000 | 9,000 | 75 | 85 | 0 |
| 85 | 95 | 50 | 150 | 9,000 | 13,000 | 85 | 95 | 0 |
| 95 | 100 | 50 | 150 | 13,000 | 18,100 | 95 | 100 | 0 |
| 100 | 105 | 50 | 150 | 18,100 | 24,100 | 100 | 105 | 0 |
| 105 | 106 | 50 | 150 | 24,100 | 26,500 | 105 | 106 | 0 |
| 106 | 115 | 50 | 150 | 26,500 | 36,000 | 106 | 115 | 0 |
| 115 | 116 | 50 | 150 | 36,000 | 41,000 | 115 | 116 | 0 |
| 116 | 120 | 50 | 150 | 41,000 | 45,000 | 116 | 120 | 0 |
| 120 | 121 | 50 | 150 | 45,000 | 52,000 | 120 | 121 | 0 |
| 121 | 130 | 50 | 150 | 52,000 | 68,000 | 121 | 130 | 0 |
| 130 | 131 | 50 | 150 | 68,000 | 78,000 | 130 | 131 | 0 |
| 131 | 140 | 50 | 150 | 78,000 | 136,000 | 131 | 140 | 0 |
| 140 | 141 | 50 | 150 | 136,000 | 177,000 | 140 | 141 | 0 |
| 141 | 150 | 50 | 150 | 177,000 | 300,000 | 141 | 150 | 0 |
| Physical Melee Damage, Physical Ranged Damage & Tactical Offence Damage (Physical Mastery Rating & Tactical Mastery Rating) by OppLvl* | ||||||||
| 1 | 50 | 200 | 600 | 300 | 3,000 | 1 | 50 | 0 |
| 50 | 60 | 200 | 600 | 3,000 | 4,500 | 50 | 60 | 0 |
| 60 | 65 | 200 | 600 | 4,500 | 6,000 | 60 | 65 | 0 |
| 65 | 75 | 200 | 600 | 6,000 | 9,000 | 65 | 75 | 0 |
| 75 | 85 | 200 | 600 | 9,000 | 13,500 | 75 | 85 | 0 |
| 85 | 95 | 200 | 600 | 13,500 | 19,500 | 85 | 95 | 0 |
| 95 | 100 | 200 | 600 | 19,500 | 27,100 | 95 | 100 | 0 |
| 100 | 105 | 200 | 600 | 27,100 | 36,000 | 100 | 105 | 0 |
| 105 | 106 | 200 | 600 | 36,000 | 40,000 | 105 | 106 | 0 |
| 106 | 115 | 200 | 600 | 40,000 | 54,000 | 106 | 115 | 0 |
| 115 | 116 | 200 | 600 | 54,000 | 62,000 | 115 | 116 | 0 |
| 116 | 120 | 200 | 600 | 62,000 | 68,000 | 116 | 120 | 0 |
| 120 | 121 | 200 | 600 | 68,000 | 78,000 | 120 | 121 | 0 |
| 121 | 130 | 200 | 600 | 78,000 | 102,000 | 121 | 130 | 0 |
| 130 | 131 | 200 | 600 | 102,000 | 117,000 | 130 | 131 | 0 |
| 131 | 140 | 200 | 600 | 117,000 | 204,000 | 131 | 140 | 0 |
| 140 | 141 | 200 | 600 | 204,000 | 265,000 | 140 | 141 | 0 |
| 141 | 150 | 200 | 600 | 265,000 | 450,000 | 141 | 150 | 0 |
| Tactical Outgoing Healing (Tactical Mastery Rating & Outgoing Healing Rating) by CharLvl* | ||||||||
| 1 | 50 | 70 | 210 | 450 | 4,500 | 1 | 50 | 0 |
| 50 | 60 | 70 | 210 | 4,500 | 6,800 | 50 | 60 | 0 |
| 60 | 65 | 70 | 210 | 6,800 | 9,100 | 60 | 65 | 0 |
| 65 | 75 | 70 | 210 | 9,100 | 13,700 | 65 | 75 | 0 |
| 75 | 85 | 70 | 210 | 13,700 | 20,600 | 75 | 85 | 0 |
| 85 | 95 | 70 | 210 | 20,600 | 29,800 | 85 | 95 | 0 |
| 95 | 100 | 70 | 210 | 29,800 | 41,000 | 95 | 100 | 0 |
| 100 | 105 | 70 | 210 | 41,000 | 55,000 | 100 | 105 | 0 |
| 105 | 106 | 70 | 210 | 55,000 | 61,000 | 105 | 106 | 0 |
| 106 | 115 | 70 | 210 | 61,000 | 83,000 | 106 | 115 | 0 |
| 115 | 116 | 70 | 210 | 83,000 | 95,000 | 115 | 116 | 0 |
| 116 | 120 | 70 | 210 | 95,000 | 104,000 | 116 | 120 | 0 |
| 120 | 121 | 70 | 210 | 104,000 | 120,000 | 120 | 121 | 0 |
| 121 | 130 | 70 | 210 | 120,000 | 156,000 | 121 | 130 | 0 |
| 130 | 131 | 70 | 210 | 156,000 | 179,000 | 130 | 131 | 0 |
| 131 | 140 | 70 | 210 | 179,000 | 312,000 | 131 | 140 | 0 |
| 140 | 141 | 70 | 210 | 312,000 | 410,000 | 140 | 141 | 0 |
| 141 | 150 | 70 | 210 | 410,000 | 690,000 | 141 | 150 | 0 |
| Resistance (Resistance Rating) by Highest* | ||||||||
| 1 | 50 | 50 | 150 | 300 | 3,000 | 1 | 50 | 0 |
| 50 | 60 | 50 | 150 | 3,000 | 4,500 | 50 | 60 | 0 |
| 60 | 65 | 50 | 150 | 4,500 | 6,000 | 60 | 65 | 0 |
| 65 | 75 | 50 | 150 | 6,000 | 9,000 | 65 | 75 | 0 |
| 75 | 85 | 50 | 150 | 9,000 | 13,500 | 75 | 85 | 0 |
| 85 | 95 | 50 | 150 | 13,500 | 19,500 | 85 | 95 | 0 |
| 95 | 100 | 50 | 150 | 19,500 | 27,100 | 95 | 100 | 0 |
| 100 | 105 | 50 | 150 | 27,100 | 36,000 | 100 | 105 | 0 |
| 105 | 106 | 50 | 150 | 36,000 | 40,000 | 105 | 106 | 0 |
| 106 | 115 | 50 | 150 | 40,000 | 54,000 | 106 | 115 | 0 |
| 115 | 116 | 50 | 150 | 54,000 | 62,000 | 115 | 116 | 0 |
| 116 | 120 | 50 | 150 | 62,000 | 68,000 | 116 | 120 | 0 |
| 120 | 121 | 50 | 150 | 68,000 | 78,000 | 120 | 121 | 0 |
| 121 | 130 | 50 | 150 | 78,000 | 102,000 | 121 | 130 | 0 |
| 130 | 131 | 50 | 150 | 102,000 | 117,000 | 130 | 131 | 0 |
| 131 | 140 | 50 | 150 | 117,000 | 204,000 | 131 | 140 | 0 |
| 140 | 141 | 50 | 150 | 204,000 | 265,000 | 140 | 141 | 0 |
| 141 | 150 | 50 | 150 | 265,000 | 450,000 | 141 | 150 | 0 |
| Critical Defence (Critical Defence) by Highest* | ||||||||
| 1 | 50 | 80 | 240 | 200 | 2,000 | 1 | 50 | 0 |
| 50 | 60 | 80 | 240 | 2,000 | 3,000 | 50 | 60 | 0 |
| 60 | 65 | 80 | 240 | 3,000 | 4,000 | 60 | 65 | 0 |
| 65 | 75 | 80 | 240 | 4,000 | 6,000 | 65 | 75 | 0 |
| 75 | 85 | 80 | 240 | 6,000 | 9,000 | 75 | 85 | 0 |
| 85 | 95 | 80 | 240 | 9,000 | 13,000 | 85 | 95 | 0 |
| 95 | 100 | 80 | 240 | 13,000 | 18,100 | 95 | 100 | 0 |
| 100 | 105 | 80 | 240 | 18,100 | 24,100 | 100 | 105 | 0 |
| 105 | 106 | 80 | 240 | 24,100 | 26,500 | 105 | 106 | 0 |
| 106 | 115 | 80 | 240 | 26,500 | 36,000 | 106 | 115 | 0 |
| 115 | 116 | 80 | 240 | 36,000 | 41,000 | 115 | 116 | 0 |
| 116 | 120 | 80 | 240 | 41,000 | 45,000 | 116 | 120 | 0 |
| 120 | 121 | 80 | 240 | 45,000 | 52,000 | 120 | 121 | 0 |
| 121 | 130 | 80 | 240 | 52,000 | 68,000 | 121 | 130 | 0 |
| 130 | 131 | 80 | 240 | 68,000 | 78,000 | 130 | 131 | 0 |
| 131 | 140 | 80 | 240 | 78,000 | 136,000 | 131 | 140 | 0 |
| 140 | 141 | 80 | 240 | 136,000 | 177,000 | 140 | 141 | 0 |
| 141 | 150 | 80 | 240 | 177,000 | 300,000 | 141 | 150 | 0 |
| Incoming Healing (Incoming Healing Rating) by CharLvl* | ||||||||
| 1 | 50 | 25 | 75 | 200 | 2,000 | 1 | 50 | 0 |
| 50 | 60 | 25 | 75 | 2,000 | 3,000 | 50 | 60 | 0 |
| 60 | 65 | 25 | 75 | 3,000 | 4,000 | 60 | 65 | 0 |
| 65 | 75 | 25 | 75 | 4,000 | 6,000 | 65 | 75 | 0 |
| 75 | 85 | 25 | 75 | 6,000 | 9,000 | 75 | 85 | 0 |
| 85 | 95 | 25 | 75 | 9,000 | 13,000 | 85 | 95 | 0 |
| 95 | 100 | 25 | 75 | 13,000 | 18,100 | 95 | 100 | 0 |
| 100 | 105 | 25 | 75 | 18,100 | 24,100 | 100 | 105 | 0 |
| 105 | 106 | 25 | 75 | 24,100 | 26,500 | 105 | 106 | 0 |
| 106 | 115 | 25 | 75 | 26,500 | 36,000 | 106 | 115 | 0 |
| 115 | 116 | 25 | 75 | 36,000 | 41,000 | 115 | 116 | 0 |
| 116 | 120 | 25 | 75 | 41,000 | 45,000 | 116 | 120 | 0 |
| 120 | 121 | 25 | 75 | 45,000 | 52,000 | 120 | 121 | 0 |
| 121 | 130 | 25 | 75 | 52,000 | 68,000 | 121 | 130 | 0 |
| 130 | 131 | 25 | 75 | 68,000 | 78,000 | 130 | 131 | 0 |
| 131 | 140 | 25 | 75 | 78,000 | 136,000 | 131 | 140 | 0 |
| 140 | 141 | 25 | 75 | 136,000 | 177,000 | 140 | 141 | 0 |
| 141 | 150 | 25 | 75 | 177,000 | 300,000 | 141 | 150 | 0 |
| Block, Parry & Evade Chance (Block, Parry & Evade Rating) by Highest* | ||||||||
| 1 | 50 | 13 | 39 | 200 | 2,000 | 1 | 50 | 0 |
| 50 | 60 | 13 | 39 | 2,000 | 3,000 | 50 | 60 | 0 |
| 60 | 65 | 13 | 39 | 3,000 | 4,000 | 60 | 65 | 0 |
| 65 | 75 | 13 | 39 | 4,000 | 6,000 | 65 | 75 | 0 |
| 75 | 85 | 13 | 39 | 6,000 | 9,000 | 75 | 85 | 0 |
| 85 | 95 | 13 | 39 | 9,000 | 13,000 | 85 | 95 | 0 |
| 95 | 100 | 13 | 39 | 13,000 | 18,100 | 95 | 100 | 0 |
| 100 | 105 | 13 | 39 | 18,100 | 24,100 | 100 | 105 | 0 |
| 105 | 106 | 13 | 39 | 24,100 | 26,500 | 105 | 106 | 0 |
| 106 | 115 | 13 | 39 | 26,500 | 36,000 | 106 | 115 | 0 |
| 115 | 116 | 13 | 39 | 36,000 | 41,000 | 115 | 116 | 0 |
| 116 | 120 | 13 | 39 | 41,000 | 45,000 | 116 | 120 | 0 |
| 120 | 121 | 13 | 39 | 45,000 | 52,000 | 120 | 121 | 0 |
| 121 | 130 | 13 | 39 | 52,000 | 68,000 | 121 | 130 | 0 |
| 130 | 131 | 13 | 39 | 68,000 | 78,000 | 130 | 131 | 0 |
| 131 | 140 | 13 | 39 | 78,000 | 136,000 | 131 | 140 | 0 |
| 140 | 141 | 13 | 39 | 136,000 | 177,000 | 140 | 141 | 0 |
| 141 | 150 | 13 | 39 | 177,000 | 300,000 | 141 | 150 | 0 |
| Partial Block, Parry & Evade Chance (Block, Parry & Evade Rating) by Highest* | ||||||||
| 1 | 50 | 25 | 75 | 350 | 3,500 | 1 | 50 | 0 |
| 50 | 60 | 25 | 75 | 3,500 | 5,300 | 50 | 60 | 0 |
| 60 | 65 | 25 | 75 | 5,300 | 7,100 | 60 | 65 | 0 |
| 65 | 75 | 25 | 75 | 7,100 | 10,700 | 65 | 75 | 0 |
| 75 | 85 | 25 | 75 | 10,700 | 16,100 | 75 | 85 | 0 |
| 85 | 95 | 25 | 75 | 16,100 | 23,300 | 85 | 95 | 0 |
| 95 | 100 | 25 | 75 | 23,300 | 32,000 | 95 | 100 | 0 |
| 100 | 105 | 25 | 75 | 32,000 | 43,000 | 100 | 105 | 0 |
| 105 | 106 | 25 | 75 | 43,000 | 47,000 | 105 | 106 | 0 |
| 106 | 115 | 25 | 75 | 47,000 | 65,000 | 106 | 115 | 0 |
| 115 | 116 | 25 | 75 | 65,000 | 75,000 | 115 | 116 | 0 |
| 116 | 120 | 25 | 75 | 75,000 | 81,000 | 116 | 120 | 0 |
| 120 | 121 | 25 | 75 | 81,000 | 93,000 | 120 | 121 | 0 |
| 121 | 130 | 25 | 75 | 93,000 | 122,000 | 121 | 130 | 0 |
| 130 | 131 | 25 | 75 | 122,000 | 140,000 | 130 | 131 | 0 |
| 131 | 140 | 25 | 75 | 140,000 | 244,000 | 131 | 140 | 0 |
| 140 | 141 | 25 | 75 | 244,000 | 320,000 | 140 | 141 | 0 |
| 141 | 150 | 25 | 75 | 320,000 | 540,000 | 141 | 150 | 0 |
| Partial Block, Parry & Evade Mitigation (Block, Parry & Evade Rating) by Highest* | ||||||||
| 1 | 50 | 35 | 105 | 350 | 3,500 | 1 | 50 | 0.1 |
| 50 | 60 | 35 | 105 | 3,500 | 5,300 | 50 | 60 | 0.1 |
| 60 | 65 | 35 | 105 | 5,300 | 7,100 | 60 | 65 | 0.1 |
| 65 | 75 | 35 | 105 | 7,100 | 10,700 | 65 | 75 | 0.1 |
| 75 | 85 | 35 | 105 | 10,700 | 16,100 | 75 | 85 | 0.1 |
| 85 | 95 | 35 | 105 | 16,100 | 23,300 | 85 | 95 | 0.1 |
| 95 | 100 | 35 | 105 | 23,300 | 32,000 | 95 | 100 | 0.1 |
| 100 | 105 | 35 | 105 | 32,000 | 43,000 | 100 | 105 | 0.1 |
| 105 | 106 | 35 | 105 | 43,000 | 47,000 | 105 | 106 | 0.1 |
| 106 | 115 | 35 | 105 | 47,000 | 65,000 | 106 | 115 | 0.1 |
| 115 | 116 | 35 | 105 | 65,000 | 75,000 | 115 | 116 | 0.1 |
| 116 | 120 | 35 | 105 | 75,000 | 81,000 | 116 | 120 | 0.1 |
| 120 | 121 | 35 | 105 | 81,000 | 93,000 | 120 | 121 | 0.1 |
| 121 | 130 | 35 | 105 | 93,000 | 122,000 | 121 | 130 | 0.1 |
| 130 | 131 | 35 | 105 | 122,000 | 140,000 | 130 | 131 | 0.1 |
| 131 | 140 | 35 | 105 | 140,000 | 244,000 | 131 | 140 | 0.1 |
| 140 | 141 | 35 | 105 | 244,000 | 320,000 | 140 | 141 | 0.1 |
| 141 | 150 | 35 | 105 | 320,000 | 540,000 | 141 | 150 | 0.1 |
| Mitigations | ||||||||
| Physical Mitigation (+Orc-craft, Fell-wrought) (Physical Mitigation) by Highest* | ||||||||
| Tactical Mitigation (+Fire, Lightning, Frost, Acid, Shadow) (Tactical Mitigation) by Highest* | ||||||||
| - Light Classes - | ||||||||
| 1 | 50 | 40 | 120 | 105 | 1,330 | 1 | 50 | 0 |
| 50 | 60 | 40 | 120 | 1,330 | 2,000 | 50 | 60 | 0 |
| 60 | 65 | 40 | 120 | 2,000 | 2,660 | 60 | 65 | 0 |
| 65 | 75 | 40 | 120 | 2,660 | 4,000 | 65 | 75 | 0 |
| 75 | 85 | 40 | 120 | 4,000 | 6,000 | 75 | 85 | 0 |
| 85 | 95 | 40 | 120 | 6,000 | 8,700 | 85 | 95 | 0 |
| 95 | 100 | 40 | 120 | 8,700 | 12,100 | 95 | 100 | 0 |
| 100 | 105 | 40 | 120 | 12,100 | 16,100 | 100 | 105 | 0 |
| 105 | 106 | 40 | 120 | 16,100 | 17,600 | 105 | 106 | 0 |
| 106 | 115 | 40 | 120 | 17,600 | 24,000 | 106 | 115 | 0 |
| 115 | 116 | 40 | 120 | 24,000 | 27,300 | 115 | 116 | 0 |
| 116 | 120 | 40 | 120 | 27,300 | 30,000 | 116 | 120 | 0 |
| 120 | 121 | 40 | 120 | 30,000 | 35,000 | 120 | 121 | 0 |
| 121 | 130 | 40 | 120 | 35,000 | 45,000 | 121 | 130 | 0 |
| 130 | 131 | 40 | 120 | 45,000 | 52,000 | 130 | 131 | 0 |
| 131 | 140 | 40 | 120 | 52,000 | 91,000 | 131 | 140 | 0 |
| 140 | 141 | 40 | 120 | 91,000 | 118,000 | 140 | 141 | 0 |
| 141 | 150 | 40 | 120 | 118,000 | 200,000 | 141 | 150 | 0 |
| - Medium Classes - | ||||||||
| 1 | 50 | 50 | 150 | 144 | 1,670 | 1 | 50 | 0 |
| 50 | 60 | 50 | 150 | 1,670 | 2,500 | 50 | 60 | 0 |
| 60 | 65 | 50 | 150 | 2,500 | 3,300 | 60 | 65 | 0 |
| 65 | 75 | 50 | 150 | 3,300 | 5,000 | 65 | 75 | 0 |
| 75 | 85 | 50 | 150 | 5,000 | 7,500 | 75 | 85 | 0 |
| 85 | 95 | 50 | 150 | 7,500 | 10,800 | 85 | 95 | 0 |
| 95 | 100 | 50 | 150 | 10,800 | 15,100 | 95 | 100 | 0 |
| 100 | 105 | 50 | 150 | 15,100 | 20,100 | 100 | 105 | 0 |
| 105 | 106 | 50 | 150 | 20,100 | 22,100 | 105 | 106 | 0 |
| 106 | 115 | 50 | 150 | 22,100 | 30,000 | 106 | 115 | 0 |
| 115 | 116 | 50 | 150 | 30,000 | 34,000 | 115 | 116 | 0 |
| 116 | 120 | 50 | 150 | 34,000 | 37,000 | 116 | 120 | 0 |
| 120 | 121 | 50 | 150 | 37,000 | 43,000 | 120 | 121 | 0 |
| 121 | 130 | 50 | 150 | 43,000 | 57,000 | 121 | 130 | 0 |
| 130 | 131 | 50 | 150 | 57,000 | 65,000 | 130 | 131 | 0 |
| 131 | 140 | 50 | 150 | 65,000 | 113,000 | 131 | 140 | 0 |
| 140 | 141 | 50 | 150 | 113,000 | 147,000 | 140 | 141 | 0 |
| 141 | 150 | 50 | 150 | 147,000 | 250,000 | 141 | 150 | 0 |
| - Heavy Classes - | ||||||||
| 1 | 50 | 60 | 180 | 200 | 2,000 | 1 | 50 | 0 |
| 50 | 60 | 60 | 180 | 2,000 | 3,000 | 50 | 60 | 0 |
| 60 | 65 | 60 | 180 | 3,000 | 4,000 | 60 | 65 | 0 |
| 65 | 75 | 60 | 180 | 4,000 | 6,000 | 65 | 75 | 0 |
| 75 | 85 | 60 | 180 | 6,000 | 9,000 | 75 | 85 | 0 |
| 85 | 95 | 60 | 180 | 9,000 | 13,000 | 85 | 95 | 0 |
| 95 | 100 | 60 | 180 | 13,000 | 18,100 | 95 | 100 | 0 |
| 100 | 105 | 60 | 180 | 18,100 | 24,100 | 100 | 105 | 0 |
| 105 | 106 | 60 | 180 | 24,100 | 26,500 | 105 | 106 | 0 |
| 106 | 115 | 60 | 180 | 26,500 | 36,000 | 106 | 115 | 0 |
| 115 | 116 | 60 | 180 | 36,000 | 41,000 | 115 | 116 | 0 |
| 116 | 120 | 60 | 180 | 41,000 | 45,000 | 116 | 120 | 0 |
| 120 | 121 | 60 | 180 | 45,000 | 52,000 | 120 | 121 | 0 |
| 121 | 130 | 60 | 180 | 52,000 | 68,000 | 121 | 130 | 0 |
| 130 | 131 | 60 | 180 | 68,000 | 78,000 | 130 | 131 | 0 |
| 131 | 140 | 60 | 180 | 78,000 | 136,000 | 131 | 140 | 0 |
| 140 | 141 | 60 | 180 | 136,000 | 177,000 | 140 | 141 | 0 |
| 141 | 150 | 60 | 180 | 177,000 | 300,000 | 141 | 150 | 0 |
(*) speculative
Rating Graphs
Critical Rating
Finesse Rating
Mastery (Physical/Tactical) Ratings
Outgoing Healing Rating
Resistance Rating
Note: The results of rating penetration effects as exists in T2-5 instances, are not shown in this graph. See Stat Caps for the adjusted rating values.
Critical Defence Rating
Incoming Healing Rating
Avoidance (Block/Parry/Evade) Ratings
Note: The results of rating penetration effects as exists in T2-5 instances, are not shown in these graphs. See Stat Caps for the adjusted rating values.
Mitigation (Physical/Tactical) Ratings
Note: The results of rating penetration effects as exists in T2-5 instances, are not shown in these graphs. See Stat Caps for the adjusted rating values.